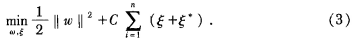壓力傳感器的輸出特性易受到環境因素，尤其是溫度變化的影響。 針對該問題 ，提出了利用支持向量機(SVM ) 對壓力傳感器輸出特性進行非線性補償 的校正模型。 校正模型利用 SVM的回歸算法來逼近非線性函數的特點 ， 通過建立壓力傳感器輸出特性與其實際電壓值之間非線性映射關 系的校正模型來實現壓力傳感器的校正。實例表明：該方法能有效地減少溫度變化對傳感器輸出的影響 ，且校正后的壓力傳感器具有更高的測量精度和溫度穩定性。

0 引 言

      在數據采集與測控系統中， 由于壓力傳感器具有結構簡單、靈敏度高、動態響應特性好、抗過載能力強等一系列優點，得到了廣泛的應用。 但壓力傳感器對溫度等環境參數較為敏感，這些因素在實際環境中總是相互關聯的，給測量結果帶來了誤差，嚴重影響了傳感器的線性度，致使其準確度大大下降。為了提高傳感器的性能， 必須對其進行校正。 但各種干擾因素對測量結果的影響很難用簡單的函數表達式來描述 ，因此 ，建立傳感器的輸出特性校正模型并求解模型往往 比較繁瑣 。

支持 向量機 ( support vector m achine ，SV M ) 是2O世紀90年代中期提出的一種機器學習算法，它建立在統計學習理論的基礎上 。 傳統的學習算法(如神經網絡) 采用的是經驗風險最小化 (ERM) 準則 ， 容易出現過擬合或者 欠擬合現象 。 SV M 以結構風 險最小化 (SR M ) 為準則 ， 對于有限樣本學習 問題 已經表現 出很多優于 已有方法 的性能 。 同時 SV M 算法是一個凸二次優化問題 ，能夠保證找 到的極值解就是全局最優解 ， 能較 好地 解決 小樣 本 、非線性和高維數的問題。 本文針對傳感器非線性誤差校正的需求，提 出了一 種壓力傳感器的SVM 非線性回歸模型。

1 S V M 校正傳感器原理

1. 1 校正原理

設壓力傳感器的數學模型為

      其中，為待測目標參數，為溫度值， y為傳感器的輸出。式(1)存反函數， 即X=f - (Y ， T ) ，但其反函數很難使用具體的函數來描述，可以利用SV M來逼近這種非線 函數。

      SVM 校正模型的原理為： 利用非線性映射將輸入的數據映射到高維空間，在高維空間變換后進行回歸分析，將目標參量測量傳感器的輸出與溫度變化等非目標參量敏感元件的輸出作為SVM校正模型的輸入，將壓力標定值作為模型的輸出，以此來減少溫度變化等非目標參量對被測目標參數的影響。 利用SVM校正壓力傳感器的原理。

1.2 SV M非線性回歸模型

      利用SVM校正模型來校正壓力傳感器，其實質是非線性回歸問題 -5 。 即利用 數學方法建立因變量與自變量之間 回歸關系函數表達式 (稱回歸方程) 。將 SVM應用到回歸分析中，需要定義不敏感損失函數s，該函數可以忽略真實值上下范圍內的誤差。 變量度量了訓練點上誤差的代價，在s不敏感區內的誤差為0 。 損失函數的解以函數的最小化為特征 ，使用 不敏感函數 可 以確保全 局最小 值 的存在和可靠泛化界的優化。

圖 2 顯示了非線性回歸函數的不敏感區函數 。

圖 2 ￡·不 敏 感 區 函數

可以用下面的SVM非線性回歸來建立壓力傳感器的非線性回歸模型

設壓力傳感器的數據樣本集為，xi yi= 1 ，n ，其 中輸入 R ，需要求解 的回歸 函數可 以表示為

根據結構最小化 準則 ，可 以將式 (2 ) 轉換為如下 的優化 問題

其約束條件為

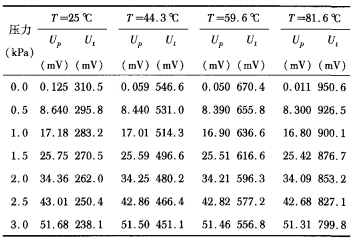
       式 (3) 中的第一項使得回歸函數更加光滑，有助于提高泛化能力，第二項可以減少誤差 。 C 為懲罰系數， C 越大表示對訓練誤差大于 s 的數據樣 本 的懲 罰越大 。 s 規定 了回歸 函數與輸 出的誤差要求 ， 越小 ， 回歸 函數與輸 出的誤差越小 ，估計精度越高 。

      目前 ，懲罰 系數 C 值 的選擇很難用理論方法確 定 ，要根據實際應用 的要求來確定 ，調節參數 的準則是 ： 檢查某特定加權的修正是否確實 減少 了誤差 ，并根 據實 際情 況進行 增減操作， 直到滿足設計要求。

      綜上所述 ，利用 SV M 回歸模型校正傳感器的流程為 ：

1 ) 獲取標定數據樣本 ，組成訓練樣本和測試樣本 ，并對數據歸一化 ；
2 ) 選擇適合的核函數， 確定精度誤差 s 和核函數的相關參數 ，用訓 練樣本對 SV M 模 型進行訓練 ， 確定 和 b 的值 ；
3 ) 當輸出與期望誤差值滿足要求時 ，訓練結束 ；轉到 步驟 (4 ) ，否則 ，重新調整 SV M 參數 ，轉到步驟 (2 ) ；
4) 用測試樣本對校 正模 型進 行檢 驗 ，如 果滿 足誤差要求 ，確定 SV M 模 型參數 ，結束 ，否則 ， 轉到步驟 (2 ) 。
2 傳感器校正
2 ． 1 傳感器標定數據與預處理
      訓練樣本選用 文獻 [8 ] 中不同工作環 境下 的傳 感器輸入輸出標定值 ，具體數據見表 1 ， 其中， 為壓力傳感器的輸出電壓， 為溫度傳感器的輸出電壓。

表 1 傳感器輸入輸 出標定值

為 了避免樣本 中存 在奇異樣 本數 據 ， 方便程 序處理 數據 ，需要對樣本進行歸一化預處理 ，歸一化 函數如下

2. 2 SV M 回歸建模

在經 歸一化后 的標定值 中 ，選擇 為 25 ，44． 3 ，59． 6 ℃時的標定值作 為 SV M 的訓 練樣 本 ， 為 81 ． 6 ℃ 的值 作為SV M 的校驗樣本 。 在 M atlab 中利用 SV M 工具 箱 中的 函數編寫訓練程序 ， 選 擇合 適 的 SV M 參 數 并將 訓I練樣 本 輸入SV M 進行訓練 ，并在 M atlab 中進行 了仿真 。 做 出校正前后為 25 ，44． 3 ，59． 6 ℃ 時的傳感器輸出曲線 圖 ，如圖 3 和 圖4所 示 。

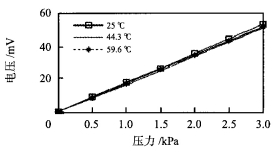
圖 3 校正前壓力傳感器的輸 出特性 曲線

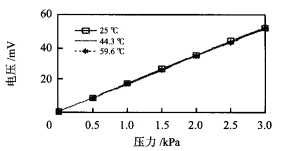
圖4 校正后壓 力傳感器的輸 出特性 曲線

      從 圖 3 和 圖4 中的曲線可 以看 出 ：經 過 SV M 回歸模 型校正的傳感器輸出曲線的線性度得到了改善 ， 回歸精度也較高 ，處 理后 數據 的最 大絕 對波動 也大 大減少 。 可見通 過校正模型處理后 ， 在相 同的溫度 變化 下 ，壓 力傳感器 的輸 出特性得 到了改善 ， 穩定性也 得到了提 高。

3 結 論
      利用 SV M 構 造傳感器 的非線性 回歸模型 ，對傳感器 的溫度影 響進行補償 ，并對非線性 誤差 進行校正 ，此方法 具有建模速度快 、校正精度高的優點。 應 用結果表 明 ：與 目前采用 的其他算法 比較 ，在 校正精 度和算 法 的推廣性 上都具 有一 定的優越性 。 但算法 中核 函數 的選擇 與其參數 的確定沒有確定 的理論依 據 ， 有待作 進一 步研究 。 通過 驗證也 可 以看出對 原始數據進行適 當的預處理 可以提高校正模 型的精度。

參考文獻 ：
[1 ] C ristianini N ，Shaw e-Taylo J． 支持 向量 機導論 [M ] ． 李 國正 ，王 猛 ，曾華 軍 ，譯 ．北京 ： 電子工業出版社 ，2004．
[2 ] V apnik V N ．統計學習理論 的本質 [M ] ． 張學工 ，譯 ． 北京 ： 清華大學出版社 ，2008．
[3 ] V apnik V ． Statistical learning theory [ M ] ． N ew Y ork ： Spr i nger，1 99 8 ．
[4 ] 李 國玉 ，孫以材 ，潘國峰 ，等．基 于 B P 網絡的壓力傳感器信 息融合 [J] ． 儀器儀表學報 ， 2005 ，26 (2 ) ：168 - 171．
[5 ] 白 鵬 ， 張 喜 斌． 基 于 支 持 向 量 機 的 壓 力 傳 感 器 校 正 模型[J] ． 空軍工程大學 學報 ： 自然 科學 版 ，2007 ，8 (5 ) ：37 —4 0 ．
[6 ] 張學 工． 關 于統 計學 習理論 與支 持向量 機 [J ] ． 自動化學 報2000 ，26 (1 ) ：32 —42 ．
[7 ] 鄧 乃揚 ， 田英杰． 數據挖 掘中 的新 方法一 支持 向量機 [ M ] ．北 京：科學 出版社 ，2004 ．
[8 ] 梁 偉鋒 ． 基 于最 小 二 乘 支持 向量 機 的壓 力 傳感 器 溫 度 補償 [J] ． 儀器儀表學報 2007 ，28 (12 ) ：2235 - 2238 ．

 班寧產品匯總